저번 시간에 Frequency Encoding 을 알아보았다. 이를 통해 x축으로의 신호 구별이 가능해졌으니, 이제 y축으로도 구별해야 한다.
오늘은 바로 그 y축 구분을 담당하는 Phase Encoding 에 대해 알아볼 것이다.
Phase Encoding 역시 기본 원리는 Frequency Encoding 과 유사하다.
Gradient 를 적용시켜 서로 다른 위상 차이를 만들어 내는 방식이다.
다들 Phase Encoding 의 개념 이해에 어려움을 겪는 편이라, 이번에는 기초적인 수준에서부터 차근차근 살펴보려 한다.

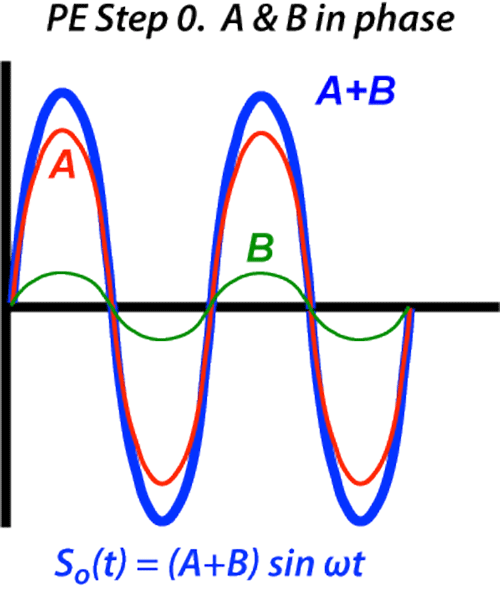
Fig 1. 의 A 와 B 픽셀은 동일한 주파수를 가지고 있다는 걸 알 수 있다.
그러나 위상은 같지 않다는 것 또한 확인할 수 있다.
그림으로만 보면 구별해낼 수 있을 것 같지만, 결국 이 신호들은 모두 합쳐지게 된다.
합쳐지는 상황을 가정하여, 같은 주파수이지만 위상이 다른 두 개의 사인파 (첫 번째 사인파는 A, 두 번째 사인파는 B) 를 한 번 더해보자.
그 결과, 위상이 다른 또 다른 사인파 (세 번째 사인파 C) 가 생길 것이다.
우리는 사인파들이 위상이 같으면 보강 간섭을 일으키고, 다르면 상쇄 간섭을 일으킨다는 사실을 알고 있다.

이 점이 중요한 것이다.
이 사인파의 합 (C) 만 보면 특정 주파수와 위상을 가진 사인파만 보일 뿐이다.
둘이 합친 신호밖에 모르기 때문에, A 의 세기와 B 의 세기는 정확히 알 수 없게 된다.
그렇다면 이번에는 y축 방향에 Gradient 를 걸어주었다가 다시 꺼보자.
이로 인해, A 는 \(Asin(\omega t)\) 으로 변화가 없고, B 는 A 보다 위상이 180도 만큼 뒤집혀서 \(-Bsin(\omega t)\ 가 되었다고 가정해보자.
이 둘이 합쳐진 신호는 \(S_1(t) = (A-B) sin(\omega t)\) 가 된다.

이 두 계산으로 인해 이제 A 와 B 를 구분할 수 있게 된다.
간단한 연립 방정식 풀이로 구할 수 있다.
\(\frac {S_0 + S_1} {2} = A\)
\(\frac {S_0 - S_1} {2} = B\)

이젠 이렇게 많아져도 껌 씹듯 풀면 된다.

Phase Step 0 에서는 아까처럼 각 주파수 별로 합만 알 수 있는 상태이다.
\(\omega_1\) 주파수 칸의 세기는 A + B
\(\omega_2\) 주파수 칸의 세기는 C + D
\(\omega_3\) 주파수 칸의 세기는 E + F
Phase Step 1 에서는 180 도 위상 차이를 부여한다면,
\(\omega_1\) 주파수 칸의 세기는 A - B
\(\omega_2\) 주파수 칸의 세기는 C - D
\(\omega_3\) 주파수 칸의 세기는 E - F
이제 다시 이 두 정보를 조합한다면 A-F 모두 알 수 있게 된다.
